CPT Q. 050: What research has been done recently on the deformational properties of mantle minerals?

Q. 50. Since the viability of the CPT model rests heavily upon the stress-strain mechanics of crustal and mantle materials, can you supply additional references for research on the dislocation creep properties of mantle minerals, beyond the one you have cited for olivine?

[Editor’s note: rough draft transcript, beta]

Response: Indeed, there is absolutely no disputing the fact that the viability of CPT depends critically upon the stress-strain behavior of mantle materials. In response to your query, yes, there are many more recent references than the ones I have cited in my papers. This field of the rheology of mantle materials is a relatively large and technical one. So I will provide some references that give a summary overview and also some that focus in on the issues particularly relevant to CPT. One of the leading and most active researchers in the field of the rheology of mantle materials is Shun-Ichiro Karato at Yale University. Many of the recent papers by him and his collaborators and students are posted on his website. A summary paper that can be downloaded from this site under the tab “Recent Publications” is one by Karato and Weidner (who is also a leading senior researcher in this field) entitled “Laboratory Studies of Rheological Properties of Minerals under Deep Mantle Conditions.”. This paper provides a relatively readable overview of the history of the experimental techniques that have been applied since the 1960’s to characterize the deformational behavior of mantle minerals and rocks under mantle-like conditions. It also emphasizes the challenges that continue to exist in this quest, especially at the pressures which exist even in the deeper parts of the upper mantle, not to mention the lower mantle. Here is the introduction from that paper:

Plastic deformation of rocks occurs during the large relative translation of rock masses that has important control over large-scale geologic phenomena such as mantle convection, plate tectonics and formation of a mountain belt. Consequently, the knowledge of rheological properties of (mantle) minerals is critical to understand these geodynamic processes.

Rheological properties that we need to know for geodynamical applications include the relationships between the creep strength (or strain-rate) and various physical/chemical parameters and the relationship between deformation microstructures and deformation conditions. In both cases, experimental studies play a major role but the experimental approach is not straightforward because of the complex nature of rheological properties and the large difference in timescale between geological deformation and deformation in laboratory experiments. Consequently, the developments of new techniques and careful evaluation of the validity of extrapolation of experimental data to geological applications have played a major role in the advancement of our knowledge on rheological properties.

In this article, we first present a brief summary of nature of experimental studies on rheological properties followed by a historical review of experimental studies of plastic deformation. Then we describe the developments of new experimental techniques at pressures beyond 10 GPa, and finally summarize the important issues that are needed to be explored. Due to the limited space, we will focus on experimental studies on rheological properties under deep mantle conditions. For a more comprehensive review, a reader is referred to other textbooks such as (Karato 2008; Poirier 1985).

I recommend this 2008 paper to help someone not that familiar with the field to acquire some general perspective, including historical perspective, on the how the deformational properties of mantle materials are experimentally determined.

For a deeper and more comprehensive view of the current state-of-the-art I recommend the textbook by Karato mentioned in the final sentence of the introduction quoted above which is entitled, Deformation of Earth Materials: An Introduction to the Rheology of the Solid Earth, published in 2008 by Cambridge University Press. Chapter 9, pp. 143-167, entitled “Dislocation creep,” is particularly relevant.

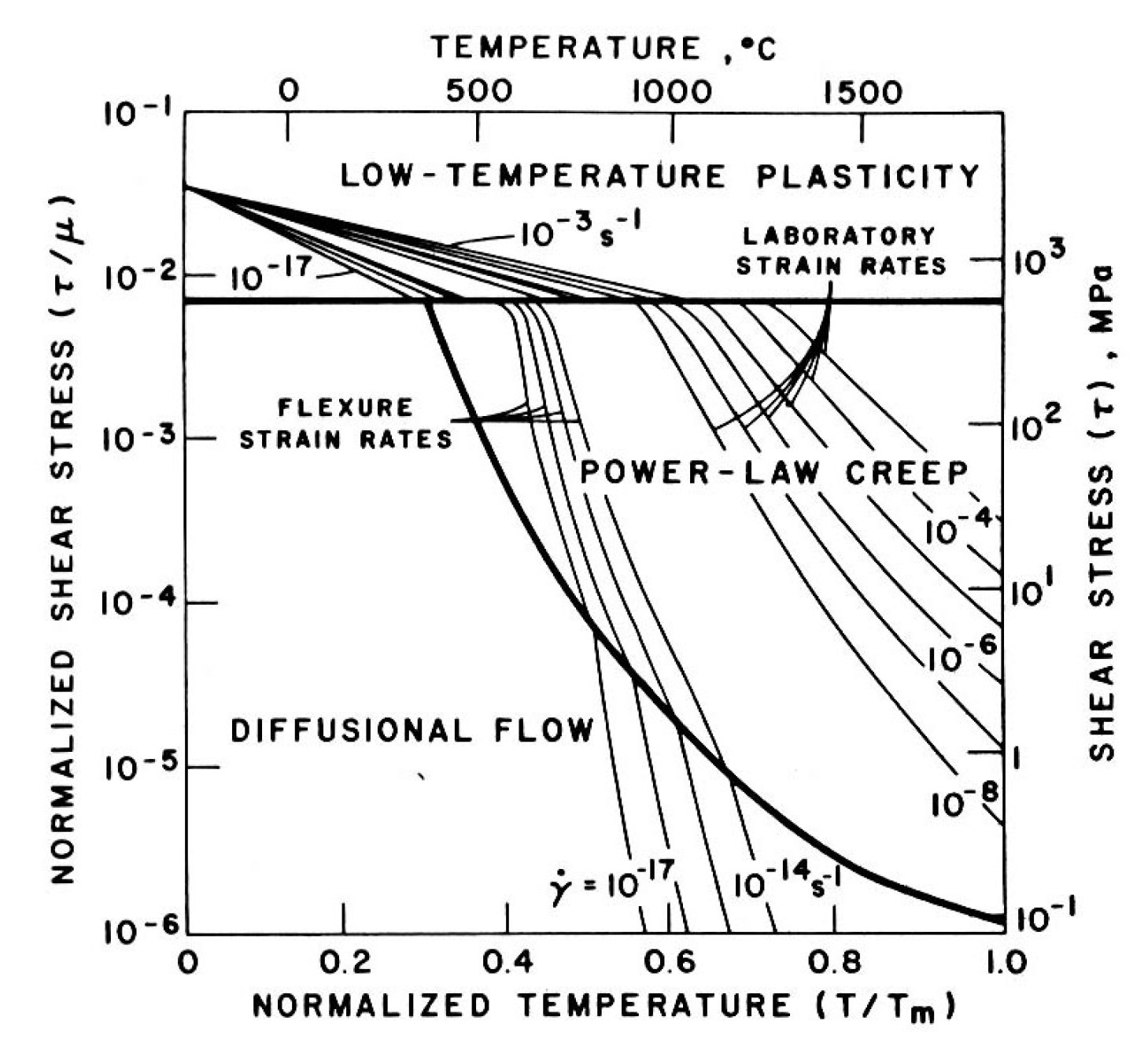
Let me now attempt to relate more recent experimental work to the primary reference I have utilized in my previous papers, namely, Kirby, S.H., “Rheology of the Lithosphere,” Rev. Geophys. Space Phys., 25, 1219-1244, 1983, including a figure from that paper shown below.

This deformation map for dry olivine with 1 mm grain size shows three main deformation regimes, namely, that of diffusional creep which occurs in the lower stress/lower temperature part of the map, that of power-law dislocation creep in the higher stress/higher temperature part of the map, and that of low-temperature plasticity for stresses above about 500 MPa (largely independent of temperature).

In my efforts to model the runaway process over the years, I have progressively included more and more realism in the deformation model. In my 1986 and 1990 ICC papers I included only the diffusional regime. In my 1994 ICC paper I added the power-law regime and consequently observed more realistic runaway behavior. Then in my 2003 ICC paper I also included the so-called low-temperature plasticity regime and obtained truly dramatic runaway results. These results were also made possible by a major advance in numerical techniques which allowed the numerical code to handle much more extreme spatial changes in rock strength. It was this discovery of the importance of the low-temperature plasticity regime that caused me to realize it is primarily this mechanism that enables the runaway process.

Since the late 1990’s this so-called ‘low-temperature plasticity’ regime in the earth science community has instead generally come to be referred as the ‘Peierls mechanism’ regime, which is more appropriate since this mechanism is largely independent of temperature. Deformation by the Peierls mechanism occurs due to glide motions, without recovery, of dislocations in the crystalline lattice. Since it appears that this mechanism is the one that is so crucial to the runaway motions in the mantle, I will focus on it in the following discussion. I will highlight a few representative papers that deal with a range of relevant issues. The first is a paper that reports results experimental deformation measurements on olivine entitled, “Low-temperature, high stress deformation of olivine under water-saturated conditions,” by I. Katayama and S. Karato, Phys. Earth Planet. Interiors, 168, 125-133, 2008. The abstract is as follows:

Low-temperature high-stress rheology of olivine was investigated under water-saturated conditions by large strain shear deformation experiments using the Griggs-type apparatus. Samples at T=1273–1373K and P = 2GPa under water-saturated conditions deformed under a significantly lower applied stress than expected from the power-law relation and the strain rate increases more rapidly with stress. These observations suggest that an exponential flow law operates under the present experimental conditions, in which the stress dependence of activation enthalpy is characterized by the Peierls stress. The Peierls stress is determined between 1.6 and 2.9 GPa depending on the choice of the form of stress dependence of the activation enthalpy. These values are significantly smaller than the Peierls stress under dry conditions (9.1GPa). We suggest that water (hydrogen) incorporated in the olivine lattices decreases the Peierls stress, and hence the rate of deformation in the exponential creep is significantly enhanced by the presence of water. The reduction of the Peierls stress by water results in the highly anisotropic weakening effect of water that causes the fabric transitions in olivine. The transition between the power-law and the exponential creep occurs at relatively low stress ∼100MPa at a geologically relevant strain rate of 10−15 s−1 when temperature is lower than 1273K and under water-rich conditions. Hence, the exponential creep might be dominated in olivine-rich rocks at low-temperature and high-stress under water-rich conditions, and such regions could be widespread in the subduction zone upper mantle where the cold lithospheric plates sink into the mantle.

The main significance of this paper is that it shows that with some water present, as many lines of evidence now indicate for the upper mantle, the threshold stress required for the Peierls mechanism to dominate the stress-strain behavior is a factor of about 3-5 lower than for the dry case. This value for wet olivine (~100 MPa) is close to what I have used in my 2D cases that yield spectacular runaway. So this experimental result is highly relevant. Below are the deformation mechanism maps summarizing the results of this study. Note the similarity of the map for dry olivine with the one shown above from the 1983 Kirby paper.

What about the other minerals of which mantle rocks are comprised? Besides olivine, the dominant upper mantle minerals are pyroxene and garnet. Laboratory measurements of the rheologies of these minerals indicate that they both are consistently stronger than olivine for essentially all upper mantle conditions. Because it is the weakest of the main constituent minerals that determines the rheology of a polycrystalline aggregate, most researchers conclude that the rheology of the upper mantle is controlled in large measure by that of olivine.

What about the lower mantle, whose dominant mineral phases are (Mg,Fe)SiO₃ perovskite and (Mg,Fe)O ferro-periclase? Important issues are the relative strengths of these two phases under lower mantle conditions. A paper entitled, “Some mineral physics constraints on the rheology and geothermal structure of Earth’s lower mantle,” by D. Yamazaki and S. Karato, American Mineralogist, 86, 385-391, 2001, shows that MgO periclase is significantly weaker than MgSiO3 perovskite. The paper’s abstract is as follows:

We explore the implications of recent mineral physics measurements of diffusion coefficients and melting temperatures of lower mantle materials on the rheological and geothermal structure of Earth’s lower mantle. We show that MgSiO3 perovskite is significantly stronger than MgO periclase and therefore the rheology of the lower mantle depends strongly on the geometry of a weaker phase, periclase. We calculate viscosities of the lower mantle for two cases: (1) where periclase occurs as isolated grains and (2) where periclase occurs as continuous films, using mineral physics data and models of two-phase rheology. We find that the effective viscosity for the former is about ~10–1000 times higher than the latter. We therefore suggest that the rheology of the lower mantle is structure- and hence strain-dependent, leading to weakening at large strains due to the formation of continuous films of periclase. Overall depth variation of viscosity depends not only on the pressure dependence of creep but also on the geothermal gradient. Both MgSiO3 perovskite and periclase have relatively small activation energies (E* = gRTm with g=10–14, where R is the gas constant and Tm is melting temperature), and therefore the depth variation of viscosity is rather small, even for a nearly adiabatic temperature gradient. However, the geothermal gradients consistent with the geodynamical inference of nearly depth-independent viscosity are sensitive to the pressure dependence of viscosity which is only poorly understood. A superadiabatic gradient of up to ~0.6 K/km is also consistent with mineral physics and geodynamical observations.

A more recent paper entitled, “Texture of (Mg,Fe)SiO₃ perovskite and ferro-periclase aggregate: Implications for rheology of the lower mantle,” by D, Yamazaki et al., Phys. Earth Planet. Interiors, 174, 139-144, 2009, deals directly with the issue of whether the periclase tends to occur as isolated grains or whether it forms continuous films. The experiments reported strongly support the latter. Therefore, because (Mg,Fe)O is several orders of magnitude weaker than (Mg,Fe)SiO₃ perovskite, its rheological properties almost certainly dominate the rheology of the lower mantle. The abstract of this paper is as follows:

Rheology of the lower mantle characterizes the dynamics of the earth’s interior and it is often controlled by the textures of the constituting material which are (Mg,Fe)SiO₃ perovskite and ferro-periclase aggregate. We conducted high-pressure experiments to synthesize the (Mg,Fe)SiO₃ perovskite and ferropericlase aggregates and measured two important textures of “grain size” and “dihedral angle”. The grain growth rates of perovskite and (ferro-)periclase in two phase aggregates were influenced by the iron content and increased with factors of ~1.5 in iron-rich system. This difference in grain growth rates indicates that the viscosity of aggregates of iron-rich system is only a few times greater than that of iron-poor system for likely diffusion creep in the lower mantle. In contrast, the change of the dihedral angle of perovskite – periclase – perovskite at triple grain junction with variation of iron content was not observed systematically, but the dihedral angle decreases from ~110° to ~105° with an increase of temperature from 1673 to 2273K. The dihedral angle of 105–110° would imply the interconnected network spatially of ferro-periclase in the aggregates and the connectivity increases with temperature. As a result, at higher temperature, ferro-periclase plays more important role for understanding the rheology of the lower mantle because ferro-periclase is a few orders of magnitude softer than (Mg,Fe)SiO₃ perovskite.

A number of other investigators have shown that the Peierls mechanism is prominent in the rheological behavior of MgO (periclase) and that the associated Peierls stress is relatively insensitive to pressure. The 2008 textbook by Karato has a deformation map on page 166 for MgO (reproduced from Frost, H.J. and Ashby, M.F., Deformation Mechanism Maps, Pergamon Press, 1982). This deformation map is very similar to those shown above for olivine, including the shape of the region and stress levels where the Peierls mechanism dominates. This map for MgO for a grain size of 0.1 mm is provided below:

One concludes, therefore, based on present experimental determinations, that extrapolating the Peierls mechanism to the rocks of the lower mantle is indeed reasonable.

In regard to first-hand knowledge of or experience with this phenomenon of strain-rate weakening, the closest I have is the man-months or years I have spent seeking to develop numerical techniques to solve the very unstable partial differential equations which describe the response when a gravitational body force acts on a volume filled with this type of material and its density varies with position. I have visited labs where the sorts of mineral physics measurements described in this discussion are performed, and I know personally some of the researchers involved, but I have not been involved directly myself in these types of measurements.